Azulejos de Poisson: parte 1
Summary
La motivación para este mini-proyecto fue no sólo para familiarizarse con el trabajo con $\tt{pygame}$, sino también para darme un campo de juego que podría enganchar en otros paquetes como $\tt{networkx}$. También quería practicar la generación de fractales. Mientras revisaba viejas notas, me encontré con las reglas de un proceso aleatorio que parecía interesante de visualizar y con potencial para convertirse en un fractal.
Introduction
Simeon Denis Poisson vivió entre 1781 y 1840, durante el final del Siglo de las Luces, un periodo de tiempo caracterizado por un cambio hacia la búsqueda del conocimiento. Fue una época de innovación con la creación de la agridulce invención de la desmotadora de algodón y la seminal del primer refresco del mundo. Contribuyendo sobre todo a la física, fue durante su trabajo sobre La Probabilitie des Jugements que le llevaría a la distribución de Poisson.
Background
Una distribución de Poisson es una distribución de probabilidad que describe el número de ocurrencias de algo que se espera en un intervalo de tiempo fijo. Este número de apariciones esperadas suele llamarse lambda $\lambda$.
Algo con una apariencia que puede describirse con una distribución de Poisson se llama proceso de Poisson y surgen por todas partes, como en las llegadas de personas a una cola. Puedes ver algunos ejemplos geniales de procesos de Poisson aquí donde verás que, de hecho, ¡son bastante comunes!
La probabilidad de que, en un intervalo de tiempo fijo, veas $k$ ocurrencias de algo tiene función de masa de probabilidad(fmp):
\begin{equation} \Pr(X=k)=\frac{\lambda^ke^{-\lambda}}{k!} \end{equation}
El valor esperado de este pmf es $E\left(X\right)=\lambda$. En otras palabras, esperamos ver lambda número de ocurrencias en el promedio.
Podemos hacer otras cosas con esta distribución. Por ejemplo, en lugar de pensar en el tiempo podríamos pensar en el espacio y jugar con que estas ocurrencias sean discretas o continuas. Problemas como éste tienen importantes aplicaciones en física y pueden verse en problemas de desintegración nuclear.
En el libro Random Networks for Communications de Massimo Franceschetti y Ronald Meester, en la introducción a los modelos de redes continuas en el capítulo 2, se nos presenta la idea de un proceso puntual “algo aleatorio” en un plano con las siguientes especificaciones:
1. Estacionariedad - la distribución de los nodos en una región del plano es la misma bajo cualquier deslizamiento de la región hacia otra parte del plano.
2. Independencia - el número de nodos en regiones separadas no se afecta mutuamente.
3. Ausencia de acumulación - Sólo puede aparecer un número finito de nodos en cualquier región acotada.
El libro también describe una forma de construir dicho cuadrado en un plano descrito por:
\begin{equation} p = \frac{\lambda}{n^2} \end{equation}
Con probabilidad $p$ y valor esperado $\lambda$ y número de cuadrados $n$ resultando en $n^2$ subcuadrados.
Como prueba de concepto, he simplificado este problema a un marco que puede adaptarse a un proceso de puntos algo aleatorio en el plano. La simplificación del modelo consiste en que puede aparecer como máximo 1 cuadrado y las regiones se definen con respecto a un área acotada del plano.
Así, en lugar de trabajar con regiones, se trabaja con subdivisiones del plano. Este problema es un subconjunto propio del problema con verdadera estacionalidad. Hemos fijado nuestra distribución de Poisson con tope.
Methods
Todo el código fue escrito en $\tt{python}$, $\tt{itertools}$ y $\tt{random}$ y visualizado usando $\tt{pygame}$. El código fue escrito en visual studio code pero se puede hacer con cualquier editor de texto. El repositorio estará disponible en github.
Poisson Tile
Definimos tal subdivisión del plano con las propiedades anteriores y la probabilidad de aparecer definida anteriormente como un azulejo de Poisson
The individual Poisson tiles were defined by an object with methods for where it is to be instantiated, the probability of it appearing and an update method. Los tamaños de los azulejos se calcularon utilizando el tamaño de la ventana y el número $n^2$ de subcuadrados deseados. La probabilidad de que un punto aparezca en el mosaico viene dada por la ecuación 1
Computation and Algorithms
Los cálculos se realizaron en dos pasos principales para calcular (1) los centros de instanciación para cada cuadrado dados $n$ y el tamaño de la pantalla y (2) la traslación necesaria para desplazar el cuadrado a la parte correcta del plano. Estas particiones del plano se visualizan mediante el cálculo por separado de las líneas horizontales y verticales de la cuadrícula generadas en una función independiente.
Calculation of Centers
Los centros se determinaron encontrando el punto medio de los subcuadros en el nivel $n$ excluyendo los puntos finales, y luego tomando todas las combinaciones de 2 pares de estos puntos medios.
Así pues, sea $C_n$ el conjunto de centros para el nivel $n$ con $n$ elementos excluyendo los puntos finales de $0$ y $E$ la arista. Un algoritmo que mapea:
\begin{equation} C_n\times C_n\rightarrow(n,n) \end{equation}
y devuelve una lista que contiene todos los centros conseguidos con $\tt{itertools}$. Debido a la simetría del cuadrado, estas tuplas definen cada punto medio de cada subcuadrado.
Calculation of Translation
Debido a cómo $\tt{pygame}$ hace una superficie y un rect, tuve que traducir el objeto rect para deslizar cada subcuadrado en su correcta subdivisión del plano. Esta subdivisión es lo que posteriormente se visualiza a través de las líneas de la cuadrícula en el cálculo final.
Los desplazamientos llamados $\delta$ se calcularon dado el tamaño de la pantalla y el número $n$ de cuadrados necesarios. Tras el cálculo se trasladaron los cuadrados a lo largo del eje x primero y luego se incrementaron a lo largo del eje y uno hasta que se colocaron todos los cuadrados. Aprovechando la forma en que se calcularon los centros sólo tuve que asegurarme de que estas traslaciones se asignaran en el mismo orden en que se calcularon los centros.
Results
change of lambda constant $n$
En esta parte de la simulación el número de azulejos se mantiene constante mientras se modifica la variable lambda. La simulación muestra que a medida que $\lambda$ aumenta de $1\rightarrow 16\rightarrow 32\rightarrow 64$, más frecuentemente aparecen los puntos en los azulejos. También puede considerarse que la probabilidad aumenta de $\frac{1}{64}$, a $\frac{1}{4}$, a $\frac{1}{2}$ a $1$. Esto aclara el porqué de la aparición de más cuadrados, ya que la probabilidad de que aparezca un cuadrado en cada azulejo aumenta. A la inversa, el punto del azulejo aparece con menos frecuencia mientras $\lambda$ disminuye.
change of $n$ with constant $\lambda$
Así es como la simulación maneja tener varios n con una tolerancia fija de $\lambda = n^2$ y así el punto siempre aparecerá en el cuadrado. En orden de izquierda a derecha, de arriba a abajo, tenemos $n=1,2,3,4$. Se puede ver que para $n$ tenemos $n^2$ fichas que aparecen. Esto significa que el programa puede llegar a ser muy caro computacionalmente para ver muy rápidamente. Mi ordenador puede manejar hasta al menos 50, pero a los 100 el programa falla debido a un error de división por cero que viene de los puntos flotantes siendo forzados a 0 para $n^2$ muy grandes.
constant ratio change


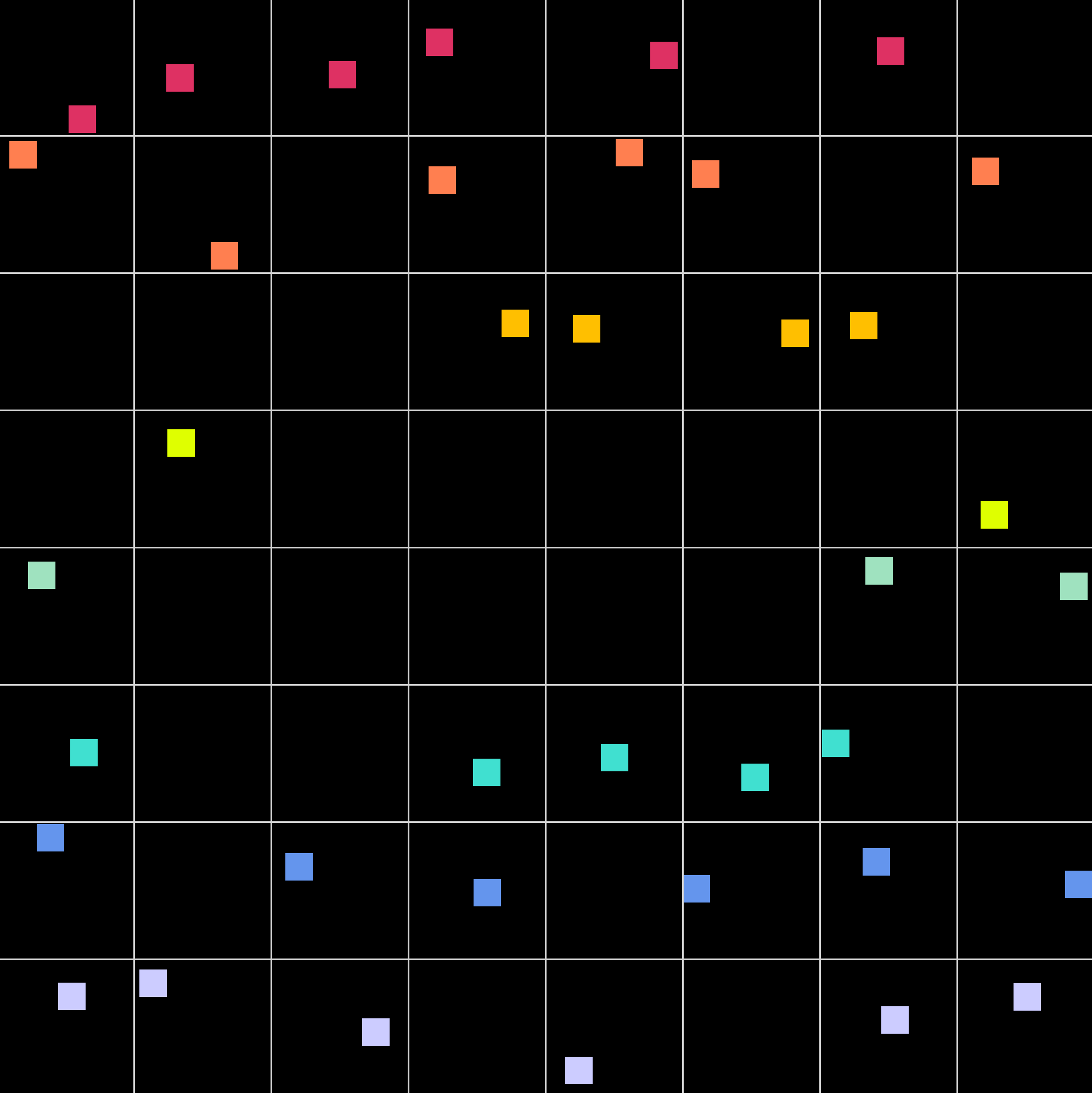
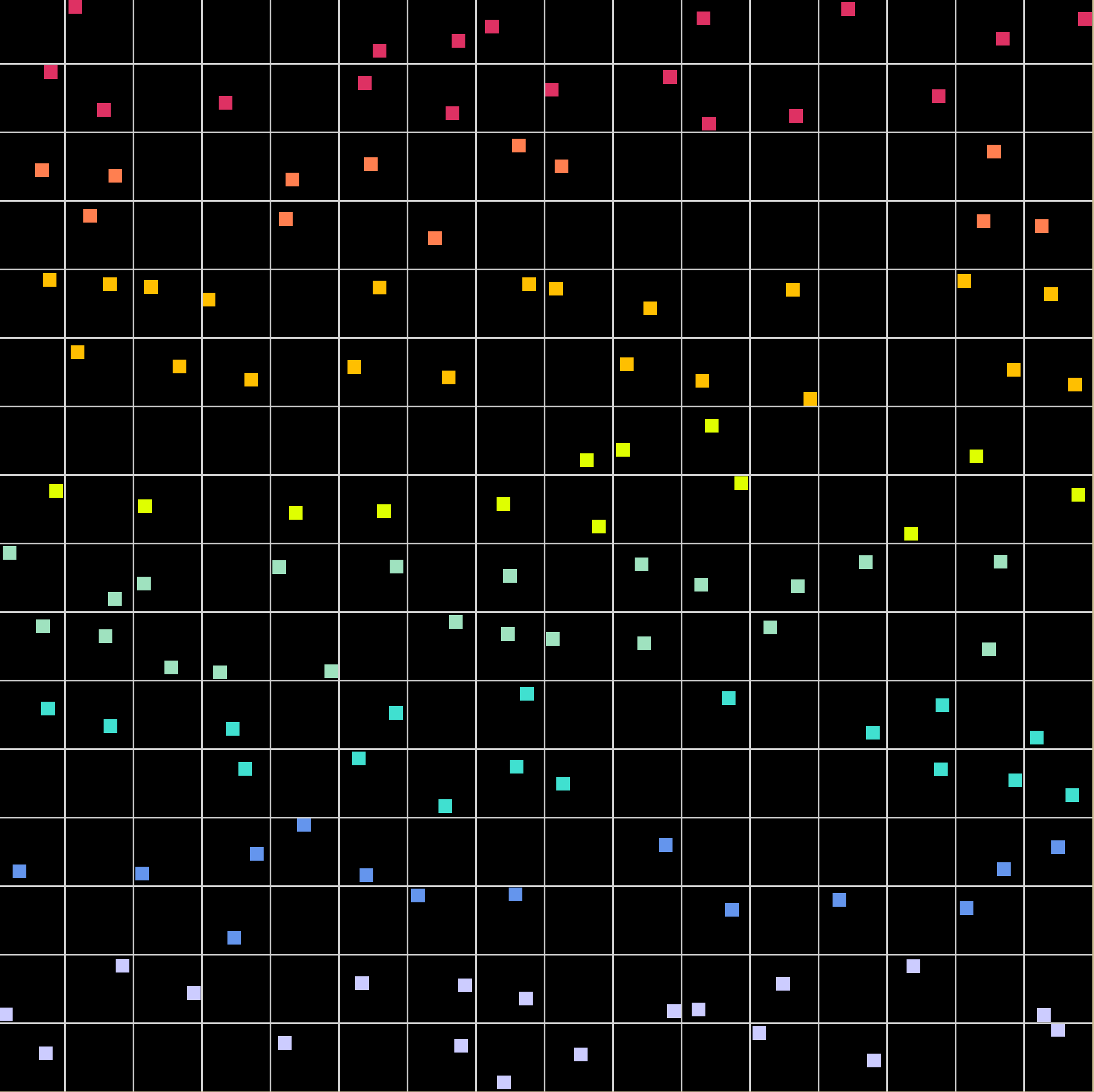
Aquí algunos patrones producidos por la simulación con un cambio de proporción constante de $\lambda = n^2/2$ para $n=1,2,3,4$. Con una probabilidad del 50% aparece un punto en un azulejo. Aquí podemos ver que obtenemos aproximadamente la mitad de los azulejos con un punto que aparece dentro de ellas mientras que en la otra mitad de los azulejos no aparece ningún punto.
Discussion
Es bastante genial que para un conjunto $\lambda$, toda la pantalla se genera a partir de un solo parámetro $n$ el progrma se genera de forma $F(n)$ = programa. En futuras actualizaciones, quiero reescribir este programa para aprovechar que se ejecuta con $\tt{pygame}$. Debe ser capaz de ser ejecutado como un ejecutable que le permite seleccionar un $n$ y ver la imagen. También me gustaría que devolviera estadísticas básicas ater incluyendo recuentos para el número de veces que un punto apareció en un cuadrado, el número medio de puntos por ciclo, etc.
Simplification and improvements
Como ya he dicho, estos azulejos son una versión más sencilla de lo que quería hacer, ya que estaba mucho más ocupado de lo que quería. El resultado es que en lugar de ser azulejos de Poisson en realidad se pueden ver como azulejos de Bernoulli. Es decir, la simulación se puede tomar como una distribución binomial de $n^2$ ensayos y $p$ de aparición. En el futuro eliminaré la simplificación y haré los azulejos de Poisson que me había propuesto inicialmente.
Hay algunas simplificaciones que se pueden hacer en el código con el fin de hacer que se ejecute más rápido y más eficiente. Esto es sería bueno para ver exactamente qué tan alto un $n $ puedo correr en mi computadora. Esto es también una cuestión de lo pequeño que puedo dividir los cuadrados por como $n^2$ aumenta $\frac{1}{n^2}$ se acerca cada vez más a cero, lo que resulta en un error desagradable de dividir por cero.
Por último, en el futuro, también me gustaría ampliar esta visualización 2D a una visualización 3D, así como solucionar un problema de sonido que hace que escuchar la simulación sea insoportable para grandes $n$. Esto podría ser un problema de los diferentes canales utilizados en $\tt{pygame}$
Conclusion
Este fue un miniproyecto divertido. Lo dejaré en suspenso por ahora porque hay otro que me gustaría empezar. Pero definitivamente quiero volver y mejorar esto. Las simulaciones de este tipo se hacen a menudo con gráficos y pueden utilizarse en el contexto de la teoría de redes para hacer comparaciones. Si la simulación es lo suficientemente aleatoria, podemos compararla con otra cosa y ver si también es lo suficientemente aleatoria y, si no lo es, podemos preguntarnos por qué. Esto surge en cosas como las percolaciones, los enlaces entre servidores o incluso la difusión de memes en twitter.